
こんにちは!
さきほど仕事で一山超えることができて、ほっと一息つきながらこの記事を書いています。
とはいえ一山と言ってもこれから続く仕事の山に比べれば公園の滑り台くらいの高さしかなく・・・アルプス山脈級の山々がこれから続いていくので、まだまだがんばらなくてはなのです💦
今朝はまた古河公方公園で散歩していたのですが、「そういえばはなももプラザに学習室があったな・・・そこで一仕事しようかな?」と思いはなももプラザへ行ってみたんですね。
しかし、入り口には大きな掲示ポスターが・・・
「学習室使用禁止」
・・・ええぇ〜!!?なにゆえ〜!?
そのポスターにはその文言と、机に大きくバツ印が書かれた絵だけが書かれています。
その「禁止」が、「ご迷惑をおかけしてすみません」とかのレベルじゃないんですよ。
「飲食禁止」とかのレベル。「迷惑だからやるなよ!」のレベルですもん。
しかも理由は何も書いていません。コロナの影響?工事中とか?
あまりに無愛想な掲示だったので、中に入って理由を聞く気も起こらず。
こうしてまた古河の生徒たちの学習の場がなくなっていることを思うと、うちの街の教育環境っていったい・・・と残念な気持ちになりました。
そして一仕事を終え、いまはそばカフェ・ほどほどにて記事を書いています。
ほどほどには久しぶりに来たかも。たまにしか来られないのですが、けっこう気に入っている場所の一つです。
甘いものが欲しかったので、ブルーハワイクリームソーダを注文。

こういうのインスタ映えっていうんですかね〜。インスタやってないですけど。
クリームがおいしかったです。満足満足。
そう言えば以前に「古河の学習塾あるあるシリーズ」という記事を書いていたのですが
続きにできそうな出来事を最近見つけた来たので、それについて書こうと思います!
(忘れていたわけではないですよ笑)
2×aとa²を間違える生徒が後を絶たない問題・・・
タイトルの通りなのですが、2×aとa²を間違える生徒が多いのです。
2×aは、aを2倍しているもの。
a²はaを2回かけているもの。
同じようで全然違いますよね。
ところがどういうわけか間違って覚える生徒の多いこと・・・。
「a=3のとき、a²の値を答えなさい。
→2×3=6」
みたいなね。
授業中に指摘すると、「あ、間違っちゃった〜♪てへぺろ♪」みたいな反応をする生徒がいるのですが・・・いやいや、これ日常生活でやったら大変なことになりますからねー。
たとえばお母さんに買い物を頼まれたとしましょう。
「帰りに牛乳2本買ってきてー」
「はーい
(牛乳1本だと150円だから、2本で2×150=300円だ。あとでお金もらっておこうと)」
となるところが、2乗と間違って覚えていたら・・・
「帰りに牛乳2本買ってきてー」
「はーい
(牛乳1本150円だから、2本で150×150=22500円だ。牛乳たけー。あ、ってことは2本じゃなくて150本買うってことなのかな。)」
2時間後・・・
「おかあさーん。牛乳150本買ってきたよー。」
「え!?150本!?」
「1人じゃ運べないから、トラックで持ってきてもらったよー。あと全部は払えなかったから、お金ちょうだーい。」
・・・カオスですね
冷蔵庫に入り切らなかった牛乳たちはどうすればいいのでしょうか。
お風呂に入れて牛乳風呂ですかね。貴族の遊びですねー。
・・・んなわけあるかー!!!
2本と2乗を間違えただけで大惨事です。その22500円はお年玉で返済することになるでしょう。
このように、「倍」と「乗」は似て非なるものなのです。
累乗が出てくるのは中学一年生なので、一年生は間違いが多いです。
では二年生や三年生は間違えないかというと・・・うーん。受験生でも間違える子がいるのが現実です。
特に間違えやすいのが、円周と円の面積のところですね。
半径の2倍と、半径の2乗は違う!
円周は、「半径×2×円周率」
円の面積は、「半径×半径×円周率」
小学校で習った公式です。
「それくらい知ってるよー」という生徒さんもいるかと思いますが・・・
こういう問題はちゃんと解けますか??
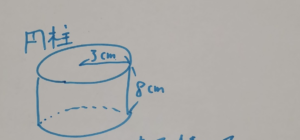
この円柱の体積と表面積はどう求めたらいいでしょうか?
(ここでどういう解き方をしたらいいか、少し考えてみてください。考えないで下にスクロールした人は、コンピューターウイルスに感染するようになっています(嘘ですw))
【答え】
底面積は円の面積になるから、半径3cm×半径3cm×π=9π㎠
よって体積は底面積×高さ=9π㎠×8cm=72π㎤
表面積は底面積が二つと、側面積の合計
側面積は長方形になるが、長方形の横の長さは底面積の円周に等しいので、半径3cm×2×π=6πcm。
よって側面積=底面積の円周×円柱の高さ=6πcm×8cm=48π㎠
表面積=底面積2つ分+側面積=9π㎠×2+48π㎠=66π㎠
答え方は合っていたでしょうか。
注目すべきは上の線を引いた部分。
ここをごちゃまぜにして書く生徒が多いです。
底面積=半径3cm×2×π=6π㎠・・・・だとか
円周=半径3cm×半径3cm×π=9π㎠・・・だとか。
2倍と2乗の違いを理解していないと、こういうミスを簡単にしてしまいます。
今後こういうミスをしたら、毎回150本の牛乳が自宅に届けられると覚悟しましょう笑
まとめ 〜2倍と2乗は、具体例で覚えるといいのかも〜
ここまで2倍と2乗の違いについてお話ししてきました。
紙の上のこととして考えると間違いやすいですが、先程の牛乳の例のように具体的な数字で考えると実感が湧くと思います。
この累乗というものは中2、中3でも扱いますし、なんなら高校でも普通に出てきます。
そのたびに「あれ、これって2倍すればいいんだっけ??」なんて考えていたら、タイムオーバーになることでしょう。
こういうのは考えなくても解けるレベルにまで持っていくべきなのです。
さっきの体積や表面積での話や、文章題でもよく出てくる数式なので、知識が怪しい方はいますぐ対策しましょう!






